Content

Pharmacokinetic modeling

• Estimate external exposure to internal dose

Probabilistic modeling

• Characterize uncertainty and variability

Sensitivity analysis

• Quantify the uncertainty from model input to model output

From toxicology to risk assessment

Pharmacokinetics (PK)

Pharmacokinetics Model

To "predict" the cumulative does by constructed compartmental model.

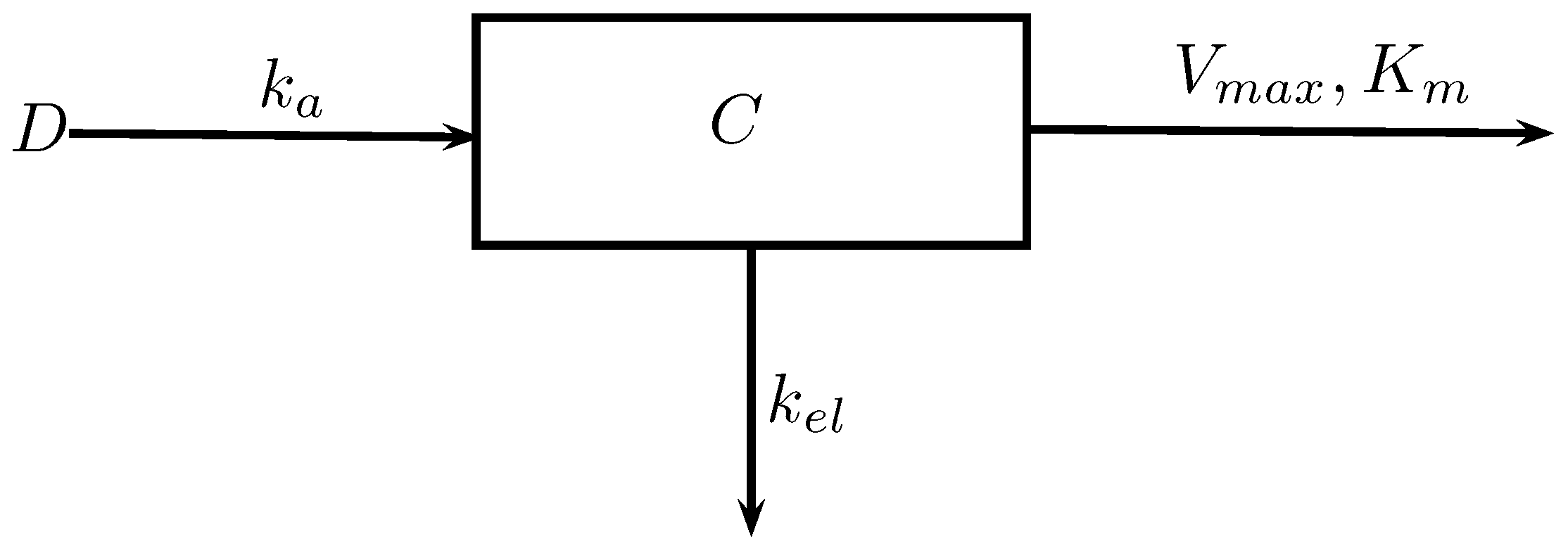
$D$: Intake dose (mass)

$C$: Concentration (mass/vol.)

$k_a$: Absorption rate (1/time)

$V_{max}$: Maximal metabolism rate

$K_m$: Concentration of chemical achieve half $V_{max}$ (mass/vol.)

$k_{el}$: Elimination rate (1/time)

Physiologically-Based Pharmacokinetic (PBPK) Model

Mathematically transcribe physiological and physicochemical descriptions of the phenomena involved in the complex ADME processes.

Img: http://pharmguse.net/pkdm/prediction.html

Why Pharmacokinetic Modeling

• Health risk assessment

• Pharmaceutical research

• Drug development

  .  
  .  
  .  
  

https://doi.org/10.1002/psp4.12134

Bayesian Population Model

Individuals level

$E$: Exposure

$t$: Time

$\theta$: Specific parameters

$y$: condition the data

Population level

$\mu$: Population means

${\Sigma }^2$: Population variances

${\sigma }^2$: Residual errors

Variability & Uncertainty

Population pharmacokinetics

ggplot(Theoph, aes(x = Time, y =conc, color = Subject)) + 
  geom_point() + geom_line() + 
  labs(x = "Time (hr)", y = "Concentration (mg/L)")

Markov-chain Monte Carlo (MCMC) simulation

Priors, posteriors, likelihood, multilevel models

$p\left(\theta |y\right)\propto p\left(y|\theta \right)\times p\left(\theta \right)$

Related publication

Luo Y-S, Hsieh N-H, Soldatow VY, Chiu WA, Rusyn I. 2018. Comparative analysis of metabolism of trichloroethylene and tetrachloroethylene among mouse tissues and strains. Toxicology 409(1): 33-43.

Luo Y-S, Cichocki JA, Hsieh N-H, Lewis L, Threadgill DW, Chiu WA, Rusyn I. Using collaborative cross mouse population to fill data gaps in risk assessment a case study of population-based analysis of toxicokinetics and kidney toxicodynamics of tetrachloroethylene. (Accepted)

Challenge

Currently, the Bayesian Markov chain Monte Carlo (MCMC) algorithm is a effective way to do population PBPK model calibration.

BUT

Possible solutions

Project

Funder: Food and Drug Administration (FDA)

Project Start: Sep-2016

Name: Enhancing the reliability, efficiency, and usability of Bayesian population PBPK modeling

• Specific Aim 1: Develop, implement, and evaluate methodologies for parallelizing time-intensive calculations and enhancing a simulated tempering-based MCMC algorithm for Bayesian parameter estimation
  (Revise algorithm in model calibration)

• Specific Aim 3: Design, build, and test a user-friendly, open source computational platform for implementing an integrated approach for population PBPK modeling
  (User friendly interface)

GNU MCSim

February 19th, 2019 - Release of GNU MCSim version 6.1.0.

Version 6.1.0 offers an automatic setting of the inverse-temperature scale in simulated tempering MCMC. This greatly facilitates the uses of this powerful algorithm (convergence is reached faster, only one chain needs to be run if inverse-temperature zero is in the scale, Bayes factors can be calculated for model choice).

Related publication

• Hsieh N-H, Reisfeld B, Bois FY and Chiu WA. 2018. Applying a Global Sensitivity Analysis Workflow to Improve the Computational Efficiencies in Physiologically-Based Pharmacokinetic Modeling. Frontiers in Pharmacology 9:588.

• Bois FY, Hsieh N-H, Gao W, Reisfeld B, Chiu WA. Well tempered MCMC simulations for population pharmacokinetic models. (Submitted)

Proposed Solution - Parameter Fixing

We usually fix the "possible" non-influential model parameters through "expert judgment".

BUT

This approach might cause "bias" in parameter estimates and model predictions.

Why we need SA?

Parameter Prioritization

• Identifying the most important factors

• Reduce the uncertainty in the model response if it is too large (ie not acceptable)

Parameter Fixing

• Identifying the least important factors

• Simplify the model if it has too many factors

Parameter Mapping

• Identify critical regions of the inputs that are responsible for extreme value of the model response

Classification of SA Methods

http://evelynegroen.github.io

"Global" sensitivity analysis is good at parameter fixing

Variance-based methods

Variance-based methods for sensitivity analysis were first employed by chemists in the early 1970s. The method, known as FAST (Fourier Amplitude Sensitivity Test).

Main effect

$$S_i=\frac{V\left[E\left(Y|X_i\right)\right]}{V\left(Y\right)}$$ $$S_i=Corr(Y,E(Y|X_i\left)\right)$$

Total effect

Example of parameter 1 for model with three parameters

$$S_{T1}=S_1+S_{12}+S_{13}+S_{123}$$

$$S_1+S_2+S_3+S_{12}+S_{13}+S_{23}+S_{123}=1$$

The basic step to performing sensitivity analysis

1. Define the variable of interest $\left(y_{j,t}\right)$

2. Identify all model factor $\left(x_i\right)$ which should be consider in GSA

3. Characterise the uncertainty for each selected input factor $p\left(x_i\right)$

4. Generate a sample of a given size $\left(n\right)$ from the previously defined probability distribution

5. Execute the model for each combination of factor

6. Visualiza the output, and interpret the outputs

7. Estimate the sensitivity measures

$$f\left(x\right)=\sin \left(x_1\right)+a{\sin }^2\left(x_2\right)+b{x}_3^4\sin \left(x_1\right)$$

x <- fast99(model = ishigami.fun, factors = 3, n = 400,
                q = "qunif", q.arg = list(min = -pi, max = pi))
par(mfrow = c(1,3))
plot(x$X[,1], x$y); plot(x$X[,2], x$y); plot(x$X[,3], x$y)

plot(x)

Challenges

(1) Many algorithms have been developed, but we don't have knowledge to identify which one is the best, and (2) there is NO suitable reference in parameter fixing for PBPK model.

ls(pos = "package:sensitivity")

##  [1] "ask"              "atantemp.fun"     "campbell1D.fun"  
##  [4] "delsa"            "dgumbel.trunc"    "dnorm.trunc"     
##  [7] "fast99"           "ishigami.fun"     "linkletter.fun"  
## [10] "morris"           "morris.fun"       "morrisMultOut"   
## [13] "parameterSets"    "pcc"              "pgumbel.trunc"   
## [16] "PLI"              "PLIquantile"      "plot3d.morris"   
## [19] "plotFG"           "pnorm.trunc"      "PoincareConstant"
## [22] "PoincareOptimal"  "qgumbel.trunc"    "qnorm.trunc"     
## [25] "rgumbel.trunc"    "rnorm.trunc"      "sb"              
## [28] "scatterplot"      "sensiFdiv"        "sensiHSIC"       
## [31] "shapleyPermEx"    "shapleyPermRand"  "sobol"           
## [34] "sobol.fun"        "sobol2002"        "sobol2007"       
## [37] "sobolEff"         "sobolGP"          "soboljansen"     
## [40] "sobolmara"        "sobolmartinez"    "sobolMultOut"    
## [43] "sobolowen"        "sobolroalhs"      "sobolroauc"      
## [46] "sobolSalt"        "sobolSmthSpl"     "sobolTIIlo"      
## [49] "sobolTIIpf"       "soboltouati"      "src"             
## [52] "support"          "tell"             "template.replace"

Materials (1/3) - Model

Acetaminophen (APAP) is a widely used pain reliver and fever reducer.

The therapeutic index (ratio of toxic to therapeutic doses) is unusually small.

Phase I (APAP to NAPQI) is toxicity pathway at high dose.

Phase II (APAP to conjugates) is major pathways at therapeutic dose.

Materials (1/3) - Model

The simulation of the disposition of acetaminophen (APAP) and two of its key metabolites, APAP-glucuronide (APAP-G) and APAP-sulfate (APAP-S), in plasma, urine, and several pharmacologically and toxicologically relevant tissues.

Zurlinden, T.J. & Reisfeld, B. Eur J Drug Metab Pharmacokinet (2016) 41: 267.

Parameters calibrated in previous study

Parameters fixed in previous study

$$V_T\frac{d{C}_T^j}{dt}=Q_T(C_A^j-\frac{C_T^j}{P_{T:blood}})$$

Materials (2/3) - Population PK Data

Materials (3/3) - Sensitivity Analysis

Morris screening

• Perform parameter sampling in Latin Hypercube following One-Step-At-A-Time

• Can compute the importance $\left({\mu }^{\ast }\right)$ and interaction $\left(\sigma \right)$ of the effects

set.seed(1111)
x <- morris(model = ishigami.fun, factors = c("Factor A", "Factor B","Factor C"), 
            r = 30, binf = -pi, bsup = pi,
            design = list(type = "oat", levels = 5, grid.jump = 3))
par(mfrow = c(1,3))
plot(x$X[,1], x$y); plot(x$X[,2], x$y); plot(x$X[,3], x$y)

par(mar=c(4,4,1,1))
plot(x, xlim = c(0,10), ylim = c(0,10))
abline(0,1) # non-linear and/or non-monotonic
abline(0,0.5, lty = 2) # monotonic
abline(0,0.1, lty = 3) # almost linear
legend("topleft", legend = c("non-linear and/or non-monotonic",
                                 "monotonic", "linear"), lty = c(1:3))

Variance-based sensitivity analysis

eFAST

Defines a search curve in the input space.

Jansen

Generates TWO independent random sampling parameter matrices.

Owen

Combines THREE independent random sampling parameter matrices.

Computational time & convergence

Time-spend in SA (min): Morris (2.4) < eFAST (19.8) $\approx$ Jansen (19.8) < Owen (59.4)

Variation of SA index: Morris (2.3%) < eFAST (5.3%) < Jansen (8.0%) < Owen (15.9%)

Consistency

Grey: first-order; Red: interaction

Parameter fixing (cut-off)

OIP: original influential parameters; OMP: original model parameters; FIP: full influential parameter; FMP: full model parameters

Parameter fixing (cut-off)

Accuracy and precision

OIP: original influential parameters; OMP: original model parameters; FIP: full influential parameter; FMP: full model parameters

Accuracy and precision

Time cost on model calibration

• Summary of the time-cost for
  • All model parameters (this study, 58),
  • GSA-judged parameters (this study, 20),
  • Expert-judged parameters (Zurlinden and Reisfeld, 2016, 21)

• All time-cost value are shown with mean and standard deviation (n = 10).

Posterior and data likelihood

Take away

• Bayesian statistics is a powerful tool. It can be used to understand and characterize the "uncertainty" and "variability" from individuals to population through data and model.

• Global sensitivity analysis can be an essential tool to reduce the dimensionality of model parameter and improve the "computational efficiency" in Bayesian PBPK model calibration.

If you want to do model calibration for PK or PBPK model, you can,

Following Work

Reproducible research - Software development (R package)

Following Work

Application of GSA in trichloroethylene (TCE)-PBPK model