Tutorial 0: GNU MCSim Introductory

# Tutorial 0: GNU MCSim Introductory
## <html>
<div style="float:left">

</div>
<hr color='#EB811B' size=1px width=796px>
</html>
### Nan-Hung Hsieh
### 2019/04/18 (update: 2019-05-29)

---

background-image: url(https://upload.wikimedia.org/wikipedia/commons/5/5a/Mcsimlogo.png)
background-size: 200px
background-position: 90% 10%

# Outline

## 1. GNU MCSim

## 2. MCSim-related publication

## 3. MCSim under R

## 4. MCSim-related R package

## 5. Workflow

???

In today's talk, I will give you a brief introduction of GNU MCSim, what it can do and how we used this software in our previous and recent research.  
Then, I will provide some information about why we use MCSim with R rather than other programming languages.   
And I'll introduce two R packages that apply MCSim to in their research workflow.  
Also, I'll provide some guidelines and workflow to explain how to use MCSim with R.

---

# What is GNU MCSim?

---

background-image: url(https://upload.wikimedia.org/wikipedia/commons/5/5a/Mcsimlogo.png)
background-size: 100px
background-position: 90% 20%

## What is GNU MCSim?

> *GNU MCSim* is a simulation and statistical inference tool for algebraic or differential equation systems. Other programs, such as *GNU Octave*, have been created to the same end. Still, most available tools are not optimal for performing computer intensive and sophisticated Monte Carlo analyses.

> *GNU MCSim* was created specifically to this end:   
> **to perform Monte Carlo analyses in an optimized, and easy to maintain environment.**

???

The GNU MCSim is simulation software. It can be used to design and use our mathematical model that is written by the algebraic or differential equation to fit or describe the data.   
But the most potent tool in MCSim is it include the Monte Carlo approach to perform Monte Carlo simulations, and Bayesian inference through Markov chain Monte Carlo simulations.  
Generally, MCSim focus on applying the Monte Carlo approach in modeling and simulation.

---

# GNU MCSim Project

- The project started by Don Maszle and [Frederic Y. Bois](https://en.wikipedia.org/wiki/Frédéric_Y._Bois) in UC Berkeley, 1991.

- First public release in 1993 (straight simulations with Monte Carlo modeling).

- Discussions with Stuart Beal at UCSF School of Pharmacy, led the team to investigate the use of **Markov chain Monte Carlo** techniques for PBPK models' calibration.

- The corresponding code was developed by Maszle, during a project in collaboration with [Andrew Gelman](https://en.wikipedia.org/wiki/Andrew_Gelman), then professor at UC Berkeley Statistics Department.

- Additional code written by Ken Revzan allowed the definition and Bayesian calibration of hierarchical statistical models.

- At the time of these developments (around 1996) those capabilities were unique for a freely distributed, easily accessible, efficient and quite versatile software.

???

The GNU MCSim project started in 1991. In the very beginning, it's a part of the Ph.D. thesis of Frederic Y. Bois.   
The primary motivation for this work was to develop and easily maintain PBPK models quickly. Because it's not convenient and easy to use C or Fortran to write the PBPK model due to this language are low level language, they are designed for the ease of the computer running the language.

Throught MCSim, they can use the easily readable model code to design the PBPK model and use MCSim to create the model program.  
They mainly used C language to write this software. The C language is the most computational efficient language at that time even in the modern world. The first public release version was available from a server at UC Berkeley.

The early version was focus on straightforward simulation with algebraic and first-order ordinary differential equations.  
It can perform a Monte Carlo simulation to understand the uncertainty in the given probability distribution of model parameters.

After that, they continuously developed more functions in MCSim, and the most important feature is the Markov Chain Monte Carlo simulation. 
It brings this software to the next level to perform the hierarchical statistical modeling and Bayesian inference.

---

background-image: url(https://i.ibb.co/nPHgMrN/MCSim-JSS.png)
background-size: 800px
background-position: 50% 40%

# GNU MCSim Project

## Published to *Journal of Statistical Software* in 1997 (version 4.2.0)

https://www.jstatsoft.org/article/view/v002i09

???

After the six years of development, they published their software to the Journal of Statistical Software in 1997.

Basically, the types of simulations in version 4.2 had included the straight simulation, Monte Carlo simulation, MCMC simulation, and setpoint simulation. These simulation functions are still available and useful in our modeling process.

---

background-image: url(https://upload.wikimedia.org/wikipedia/commons/5/5a/Mcsimlogo.png)
background-size: 100px
background-position: 90% 90%

# Version history

February 19th, 2019 - Release of GNU MCSim version 6.1.0.

>Version 6.1.0 offers an automatic setting of the inverse-temperature scale
in simulated tempering MCMC. This greatly facilitates the uses of this
powerful algorithm (convergence is reached faster, **only one chain needs** to be
run if inverse-temperature zero is in the scale, **Bayes factors** can be
calculated for model choice).

]
.font60[
- 6.0.1 (05 May 2018)
- 6.0.0 (24 February 2018)
- 5.6.6 (21 January 2017)
- 5.6.5 (27 February 2016)
- 5.6.4 (30 January 2016)
- 5.6.3 (1 January 2016)
- 5.6.2 (24 December 2015)
- 5.6.1 (21 December 2015)
- 5.6.0 (16 December 2015)
- 5.5.0 (17 March 2013)
- 5.4.0 (18 January 2011)
- 5.3.1 (3 March 2009)
- 5.3.0 (12 January 2009)
- 5.2 beta (29 January 2008)
- 5.1 beta (18 September 2006)
- 5.0.0 (4 January 2005)
- 4.2.0 (15 October 2001)
- 4.1.0 (1 August 1997)
- 4.0.0 (24 March 1997)
]

???

Until now, the latest version of GNU MCSim is 6.1. It was released on February this year.  
The recent version is focused on tempering MCMC simulation.

Generally, GNU MCSim uses Metropolis sampling in MCMC simulation to prevent the issue of conjugacy or log-concavity of prior or posterior distributions.

Therefore, it needs at least 4 independent chains to do the simulation and estimate the convergence of the model parameter. The novel approach can additionally allow the calculation of normalized densities and of Bayes factors for model comparison.

---

# Types of Simulation

.font90[
**Simple simulation**  
- Straight simulations (set parameter values and initial conditions).

**Used to:** *Model testing when building the model (e.g., mass balance)*

<hr>

**Monte Carlo simulations**  
- Perform repeated (stochastic) simulations across a randomly sampled region of the model parameter space.

**Used to:** *Check possible simulation (under given parameter distributions) results before model calibration*

<hr>

**SetPoints simulation**   
- Solves the model for a series of specified parameter sets. You can create these parameter sets yourself or use the output of a previous Monte Carlo or MCMC simulation.

**Used to:** *Posterior analysis, Local/global sensitivity analysis*
]

???

As I mentioned in the previous slide, there're different types of simulation in MCSim.  
Basically, the simple simulation used the parameters in the constructed model to estimate the output as the prediction.   
The method can be used to test your model such as mass balance in the PBPK model if you find that your input is not equal to your output.  
You might need to go back to check your equations before you use this model to do the following work.

The Monte Carlo simulation is a further step that can be used to check the possible simulation output under the given parameter distribution.  
If your data can be covered in the range of your simulations, then you can use this parameter setting in MCMC simulation.

Instead of given parameter distribution, the setPoints simulation can use the external setting of the parameter.  
We can use it to analyze the simulated result from the posterior distribution. Or we can use it to do global or local sensitivity analysis.

---

background-image: url(https://i.ibb.co/Gx6xKrq/mcmc-diagram.png)
background-size: 600px
background-position: 50% 90%

# Types of Simulation

### Markov-chain Monte Carlo (MCMC) simulation
- Performs a series of simulations along a Markov chain in the model parameter space. 
- They can be used to obtain the Bayesian **posterior** distribution of the model parameters, given a statistical model, **prior** parameter distributions and data for which a **likelihood function** can be computed. 
- *GNU MCSim* can handle hierarchical statistical models as well.

???

The most powerful and important feature in MCSim is Markov-chain Monte Carlo simulation. It performs a series of simulations along a Markov chain in the model parameter space.  
The MCMC algorithm performs the random choice of a new parameter value  (also known as posterior)  that is influenced by the previous value, which is prior.  
In this approach, we need experimental data, a generative model, parameter and prior knowledge of model parameter. Based on these three things we can estimate the Bayesian posterior parameters that are related to population and individual and further make the prediction.

---

background-image: url(https://res.cloudinary.com/dyd911kmh/image/upload/f_auto,q_auto:best/v1538685364/Ep._43_abbgvl.jpg)
background-size: 500px
background-position: 90% 80%

class:clear

## Bayesian statistics is a powerful tool, Because...
.font120[
>It gives us the opportunity to understand and quantify the .font120["uncertainty"] and .font120["variability"] from individuals to .font160[population] through **data** and **model**.
]

???

Overall, we think that Bayesian statistics is a powerful tool because it allows us to understand the uncertainty in our model and its parameters.  
It can also quantify the variability when we use hierarchical statistical modeling approach and include all experiment data such as inter-individual or inter-studies.  
Based on the Bayesian method we can estimate the population behavior according to the sample data in our hand.  
If we have more available information, we can use it to create a prediction that has high accuracy and precision.

---

class:clear, middle

<center>
--- Application ---
## If you have *known* "parameters"
## ------------------------------------>
## Parameters / Model / Data
## <------------------------------------
## If you have *known* "data" 
--- Calibration ---
???

A brief summary, there are three key elements in our modeling process. Parameters, Model, and Data.  
Here is a brief summary, if you have "known parameters" without any available data. You can use the forward method to make the prediction and used the median and 95% interval to interpret your prediction.  
But if you have "known data" and you want to calibrate your model parameters you can use the backward method, which is MCMC simulation to calibrate your model parameter and use the probability density function to explain your updated parameter.

---

# Types of Simulation

**"Optimal Design" procedure**

Optimizes the number and location of observation times for experimental conditions, in order to minimize the variance of a parameter or an output you specify, given a structural model, a statistical model, and prior distributions for their parameters

<hr>

**Systems Biology Markup Language (SBML)**

GNU MCSim can read SBML models, which provides a standard for representing biochemical pathway models. It can code for models of metabolism, cell-signaling, transcription, etc. SBML is maintained since the mid-2000 by an international community of software developers and users. 
???

Instead of the previous types of simulation, there are additional functions that had been developed in GNU MCSim.  
But currently, I haven't used or tested these functions. But just quick mention and show what additional functions that can be used in the simulation and modeling.  
The first one optimal design is used to decrease the variance of the parameter to optimize the simulation.

The other is using system biology markup language as the model file. MCSim supports the model that was written by SBML structure. So the user can use this model directly with MCSim without re-build the model under MCSim model format.

---

# What GNU MCSim can do in toxicology?

---

class:clear

## Exchange of ideas between statistics and toxicology

<hr>

### From Statistics to Toxicology

- Bayesian inference for combining prior and data

- Hierarchical models for population variation

### From Toxicology to Statistics

- Models for constrained parameters

- Hierarchical prior distributions

- New ideas in understanding and checking models

???

As I mentioned in previous slides, the MCSim can apply Bayesian statistics to estimate the model parameter and used it to perform Bayesian inference to understand and quantify the uncertainty and variability from individuals to the population.  
But this is just the points of view from statistics to toxicology.

We also need the point of view from toxicology to statistics. Therefore, the extensive knowledge from toxicology to statistics is what is the "reasonable" parameter range, how to set the model parameter from measurement value to the model parameter value.  
For example, in the PBPK model, if we have body weight measurement as information, we can make a precise prediction. Also, the detection limit in measurement instrument such as LC-MS/MS can give us the idea to set the measurement error in our model.

Therefore, it's very important to exchange ideas from both sides.

---

# What we need?

## 1. Physiological pharmacokinetic model

## 2. Hierarchical population model

## 3. Prior information

## 4. Experimental data

## 5. Bayesian inference

## 6. Computation

## 7. Model checking

???

When we started a study we might need this information. What PBPK model we have or how to build the model, how to use this PBPK model in hierarchical population modeling.

Also, we need knowledge about the model parameter as prior information. So it will be essential to know what experiment data we have. Some details in this experiment are crucial as well.

Also, we need Bayesian inference to make the prediction. We need to consider computer performance because it might take a very long time when you calibrate the model parameter.

Finally, if we make some mistake in our simulation, we need to have the ability to check our model, check our data, and check our parameter setting. All steps are very important

---

background-image: url(https://ars.els-cdn.com/content/image/1-s2.0-S027323000600095X-gr3.jpg)
background-size: 280px
background-position: 60% 80%

# Related publication

Chiu and Bois (2006) - [Revisiting the population toxicokinetics of tetrachloroethylene](https://link.springer.com/article/10.1007/s00204-006-0061-9)

Hack et al. (2006) - [Bayesian population analysis of a harmonized physiologically based pharmacokinetic model of trichloroethylene and its metabolites](https://www.sciencedirect.com/science/article/pii/S027323000600095X)

<hr>

???

There are some publications related to applied Bayesian statistics in toxicology and used MCSim as a modeling tool.

The first publication from Dr. Chiu's 2006 paper used MCSim to reanalyze the previous publication and found the more significant uncertainty of percent metabolized of perchloroethylene.

In Hack 2006 study, they applied the Bayesian approach with experimental data from animal and human studies to estimate the equivalent exposure dose that can be used to risk assessment.

This analysis provides an essential step toward estimating the uncertainty of dose-response relationships in noncancer and cancer risk assessment, improving the extrapolation of toxic TCE doses from experimental animals to humans.

---

# Related publication

Chiu and Bois (2007) - [An approximate method for population toxicokinetic analysis with aggregated data](https://link.springer.com/article/10.1198/108571107X229340)

- Applied Hierarchical Bayesian approach to estimate inter-individual variability

???

The additional research in 2007 focus on compares the hierarchical Bayesian approach for individual and aggregated datasets to estimate inter-individual variability from the observed mean and variance at each time point.

This study concludes that given information on the form of the individual-level model, useful information on inter-individual variability may be able to obtain from aggregated data.

So using the individual data or aggregated data from published paper can have the ability to make predictions through a Bayesian approach.

---

background-image: url(https://ars.els-cdn.com/content/image/1-s2.0-S0041008X09003238-gr3_lrg.jpg)
background-size: 600px
background-position: 50% 90%

# Related publication

Chiu et al. (2009) - [Characterizing uncertainty and population variability in the toxicokinetics of trichloroethylene and metabolites in mice, rats, and humans using an updated database, physiologically based pharmacokinetic (PBPK) model, and Bayesian approach](https://www.sciencedirect.com/science/article/pii/S0041008X09003238)

Chiu and Ginsberg (2011) - [Development and evaluation of a harmonized physiologically based pharmacokinetic (PBPK) model for perchloroethylene toxicokinetics in mice, rats, and humans](https://www.sciencedirect.com/science/article/pii/S0041008X11001141)

???

These are two representative publication that used the Bayesian approach in population PBPK modeling to predict the metabolic pathway of trichloroethylene and tetrachloroethylene in mice, rate, and human.

Through this modeling approach, we can predict the difference and uncertainty of metabolism of oxidation and GSH conjugation among mice, rate, and human.

---

background-image: url(https://i.ibb.co/VHT9qZ3/chiu2019.jpg)
background-size: 500px
background-position: 50% 80%

# Related publication

- Characterizing PBPK parameters from individuals to population

- Evaluating population **variability** and parameter **uncertainty**

- Cross-species comparisons of metabolism in **risk assessment**

???

A brief summarizes the Bayesian approach in population PBPK modeling. We can use it to estimate the posterior parameter. Then used the parameter uncertainty to estimate the posterior population prediction and group-specific prediction.

Based on this information we can compare the metabolism across experimental animals and human and further use this information in risk assessment.

---

background-image: url(https://i.ibb.co/tYDnPDb/chiu2014-2.png)
background-size: 500px
background-position: 80% 65%

# Related publication from our group

### Inter-strain & inter-individual variability

Chiu et al. (2014) - [Physiologically-Based Pharmacokinetic (PBPK) Modeling of Inter-strain Variability in Trichloroethylene Metabolism in the Mouse](https://ehp.niehs.nih.gov/doi/full/10.1289/ehp.1307623?url_ver=Z39.88-2003&rfr_id=ori:rid:crossref.org&rfr_dat=cr_pub%3dpubmed)

<hr>

[source](https://www.toxicology.org/groups/ss/ophss/docs/OPHSS_Webinar_ZeiseChiu_30Oct2014.pdf)

???

It is an extensive study.

Previous animal studies mainly used single strain, B6C3F1 as a representative animal. But the issue to used B6C3F1 in extrapolation is the metabolism is very difference with the human. It had the highest rate of respiratory tract oxidative metabolism as compared to rats and humans. Also, it doesn't have representative variability in risk assessment.

So in this study, instead of B6 strain, it includes 16 inbreds to discuss inter-strain variability and use it to compare with the human inter-individual variability.

Through the multi-strains model calibration and prediction, we can have consistent estimates of variability in human and mice

---

background-image: url(https://ars.els-cdn.com/content/image/1-s2.0-S0300483X18301781-gr5_lrg.jpg)
background-size: 400px
background-position: 70% 80%

# Related publication

Dalaijamts et al. (2018) - [Incorporation of the glutathione conjugation pathway in an updated physiologically-based pharmacokinetic model for perchloroethylene in mice](https://www.sciencedirect.com/science/article/pii/S0041008X18302436)

Luo et al. (2018) - [Comparative analysis of metabolism of trichloroethylene and tetrachloroethylene among mouse tissues and strains](https://www.sciencedirect.com/science/article/pii/S0300483X18301781)

Luo et al. (Accepted) - Using Collaborative Cross Mouse Population to Fill Data Gaps in Risk Assessment A Case Study of Population-based Analysis of Toxicokinetics and Kidney Toxicodynamics of Tetrachloroethylene

???

In our recent research, we incorporate more animal experiment results. The first study included an additional measurement of GSH conjugate in mice tissues, to build more comprehensive PBPK model to make Bayesian inference.

In the second and the third study we build the multicompartment PK model to estimate the metabolism of TCE and PCE in liver, kidney, brain, lung, and serum.  
We didn't use the PBPK model because the current is PBPK model takes a very long time in model calibration. Therefore, we tried to re-build this simplified model to compare and describe the Trichloroethylene and tetrachloroethylene among mouse tissues and strains.

In our third study, it is also the extensive research that used the same model with Collaborative Cross Mouse and applies the study result in risk assessment.

---

# Related publication

*U.S. Food and Drug Administration. Enhancing the reliability, efficiency, and usability of Bayesian population PBPK modeling - Create, implement, and evaluate a robust Global Sensitivity Analysis algorithm to reduce PBPK model parameter dimensionality.*

<hr>

Hsieh et al. (2018) - [Applying a Global Sensitivity Analysis Workflow to Improve the Computational Efficiencies in Physiologically-Based Pharmacokinetic Modeling](https://www.frontiersin.org/articles/10.3389/fphar.2018.00588/full)

Bois et al. (Submitted) - Well tempered MCMC simulations for population pharmacokinetic models

- Based on the latest version 6.1.0

???

This is our project from FDA that aim to improve the functionality in MCSim and the research of the Bayesian framework.

One of the current challenges in the Bayesian method is time-consuming if our model becomes more complex or more comprehensive and we have more data in our multi-individuals and multi-groups testing. It will take need very long time to calibrate model parameter. Therefore, in our 2018 paper, we proposed a workflow to fix the non-influential parameter in our PBPK model based on the global sensitivity analysis.

Through this way, we can save about half time in our model calibration.

Our recent submitted paper is to show how we developed and used tempering MCMC in PBPK modeling.  This algorithm can also have a faster convergence time compared with the original one.

---

# Inter & intra- variability modeling

<center>
.pull-left[
**Inter-individual variability model**
<img src= "https://i.ibb.co/QHMSrbq/inter.png" height="450px" />
]

.pull-right[
**Inter- & intra-individual variability model**
<img src= "https://i.ibb.co/2tzxQCN/inter-intra.png" height="450px" />
]

</center>

[source](https://link.springer.com/protocol/10.1007/978-1-62703-059-5_25)

???

In addition to inter-individual variability, the Bayesian approach can further consider the intra-individual variability.

For example, in human exposure experiment, you might use a different type or different magnitude of exposure for the specific subject, the best way to treat the data is construct the hierarchical inter- and intra-individual variability model that can have the better calibration result than consider inter-individual variability only.

In this diagram, i represent different subjects, and j represents the subject with different types of experiment.

---

# Why we use GNU MCSim with R(Studio)?

---

background-image: url(https://upload.wikimedia.org/wikipedia/commons/9/93/GPLv3_Logo.svg)
background-size: 200px
background-position: 50% 80%

# Advantages in MCSim and R

> - The freedom to run the program as you wish, for any purpose (freedom 0).
> - The freedom to study how the program works, and change it so it does your computing as you wish (freedom 1). Access to the source code is a precondition for this.
> - The freedom to redistribute copies so you can help others (freedom 2).
> - The freedom to distribute copies of your modified versions to others (freedom 3). By doing this you can give the whole community a chance to benefit from your changes. Access to the source code is a precondition for this.

???

First of all, both R and GNU MCSim are free and open source software, which means we can use this program and find all source code to understand how it works.

Also, we can revise and re-distribute the program if we have a new idea to use it. The MCSim under R is an example. We modified MCSim to run in RStudio and redistribute it as a tutorial example.

---

# Advantages in MCSim and R

**Simulation package, which allows you to:**

- design and run simulation models (using algebraic or differential equations)

- perform Monte Carlo stochastic simulations

- do Bayesian inference through Markov Chain Monte Carlo simulations

- has faster computing speed than other simulation software/packages (e.g., Asclx, Berkeley Madonna, RStan)

]

**Programming language that allows you to:**

- conduct statistical analysis (summarization, estimation)

- visualize simulation results

- use various packages to analyze results (e.g., `CODA`, `BOA`, `rstan`)

- perform sensitivity analysis (e.g., `sensitivity`, `pksensi`)

- access community support (e.g., Stack Overflow, R User groups)

]

???

I had mentioned that GNU MCSim had many powerful functions, but the worth noting feature is it has faster computational speed than other simulation software, packages, such as ... .

But through GNU MCSim we can only have simulation result that is output in the text format. So we need to use R. R is a programming language in statistical analysis. R can help us analyze and visualize the simulation result from MCSim. Also, it has various R package, so we can use it to do advanced analysis such as check the convergence of our simulations.

In addition, we can use some R packages such as sensitivity and pksensi to perform local or global sensitivity analysis. Also, if you meet any problem in your analysis, there is a lot of online resources that can help you solve the problem. ...

---

background-image: url(http://lcolladotor.github.io/figs/2016-03-07-BiocParallel/parallel.gif)
background-size: 550px
background-position: 90% 1%

# Advantages in MCSim and R

.font120[*"Parallel computing"*] 
<img src="http://lcolladotor.github.io/figs/2016-03-07-BiocParallel/cloud.jpg" height="220px" />

### - Run multiple MCMC chains with multiple CPUs

### - High performance (cloud) computing

???

Both R and MCSim are supported parallel computing, the idea of parallel computing is that we can run multiple Markov chains at the same time if your personal computer has multiple CPUs.

But using your personal computer to run MCMC simulation will burn your PC to about 90-degree Celcius. And you might not be able to do another work if you run out of your CPUs.

So basically, we used cloud computing. We build our model in our personal computer and send these files to high-performance computing server and run the simulations. It's very convenient if we have batch simulation to do.

---

background-image: url(https://i.ibb.co/VvsMMhD/Screen-Shot-2019-04-12-at-12-33-42-PM.png)
background-size: 500px
background-position: 80% 96%

class:clear

.font120[
Population pharmacokinetic reanalysis of a Diazepam PBPK model: a comparison of *Stan* and *GNU MCSim*
]

.font80[
Periklis Tsiros, Frederic Y. Bois, Aristides Dokoumetzidis, Georgia Tsiliki, Haralambos Sarimveis

- The aim of this study is to benchmark two Bayesian software tools, namely *Stan* and *GNU MCSim*, that use different Markov chain Monte Carlo (MCMC) methods for the estimation of physiologically based pharmacokinetic (PBPK) model parameters.

- The software tools were applied and compared on the problem of updating the parameters of a Diazepam PBPK model, using time-concentration human data. Both tools produced very good fits at the individual and population levels, despite the fact that *GNU MCSim* is not able to consider multivariate distributions.

- *Stan* outperformed GNU MCSim in sampling efficiency, due to its almost uncorrelated sampling.

- However, *GNU MCSim* exhibited much **faster convergence** and performed better in terms of effective samples produced per unit of time.
]

.font60[
Journal of Pharmacokinetics and Pharmacodynamics; https://doi.org/10.1007/s10928-019-09630-x

Original Paper; First Online: 04 April 2019
]
<img src= "https://i.ibb.co/XZc2tXq/HMC.png" height="150px" />

???

It's a recent published paper that compared the performance between MCSim and Stan.  
Stan is a probabilistic programming language for bayesian statistical inference written in C++. But Stan used the different smapling algorithm which call Hamiltonian Monte-Carlo to estimate posterior.

Because the sampleing algorithm in Stan is aim to prevent the parameter correlation that will slow down the speed of covergence.

The study result showed that Stan outperformed GNU MCSim in sampling efficiency, due to its almost uncorrelated sampling. But GNU MCSim had relatively high speed of convergence than Stan.

http://www.bayes-pharma.org/Abstracts2013/slides/Presentation%20Pierre%20Lebrun.pdf

---

background-image: url(https://i.ibb.co/0c8rQ4p/httk.png)
background-size: 540px
background-position: 50% 96%

# MCSim-related R packages

**httk: R Package for High-Throughput Toxicokinetics**

> *MCSim* (Bois and Maszle 1997) was used for converting the model equations into C code, which is used with **deSolve** (Soetaert et al. 2016) in solving each system of equations.

*GNU MCSim* model code

C code

**deSolve**

Prediction

???

One of the MCSim related R package is httk.  
It used MCSim to transfer the model code to C code. And then use deSovle R package to solve differential equation and make prediction.

In httk, it has three built-in models that was preliminary written from MCSim model format. It also includes chemical-specific in vitro data from relatively high throughput experiments.  
These functions and data provide a set of tools for in vitro-in vivo extrapolation.

---

# MCSim-related R packages

**pksensi:  R Package for Global Sensitivity Analysis in Pharmacokinetic Modeling**

>pksensi implements the global sensitivity analysis workflow to investigate the parameter uncertainty and sensitivity in pharmacokinetic (PK) models, especially the physiologically based pharmacokinetic (PBPK) model with multivariate outputs. The package also provides some functions to check the convergence and sensitivity of model parameters.

.right[[![CRAN\_Status\_Badge](http://www.r-pkg.org/badges/version-last-release/pksensi)](https://cran.r-project.org/package=pksensi)]

**Two types of model solver**

`solve_fun()` 
*GNU MCSim* model code

C code

**deSolve**

Prediction

`solve_mcsim()` 
*GNU MCSim* model code

Prediction
 
**Note:** `solve_mcsim()` is faster than `solve_fun()`

???

Based on our publication in 2018, we further develop an R package called pksensi, this package aims to help us reproduce the publish result and provide a convenient way for modelers who want to apply our global sensitivity approach in their study.

We adopt the idea from the httk package so the user can use the deSolve R package to perform sensitivity analysis. However, this method is not computationally efficient. It takes a long time to solve the ODE from the parameter matrix that we generate from the specific sensitivity analysis algorithm.

The alternative solution is used MCSim model file and create model program then use it to predict the model output to have a faster speed than deSovle.

---

background-image: url(http://devhumor.com/content/uploads/images/November2017/step-by-step-debugging.png) 
background-size: 450px 
background-position: 95% 90%

# Disadvantages in MCSim and R

### Difficult learning curve (command line interface-based)

### Requires coding/programming skill

### Requires installation of extra program or package

### Requires **"debugging"**

???

Next, I will talk about some disadvantage of MCSim and R. Both this software are running in the coding and programming environment, which means the user needs to spend their time to learn this language.  
Basically, It is not easy for the beginner who is familiar with graphic user interface and used it in daily work. Also, it's easy to meet a lot of problem at the beginning. So the user needs to install an extra program such as Rtools and additional package to do analysis.  
It also requires an additional setting in the working environment. There are a lot of debugging works to do. For example, you might make some mistake in your equation, but you never notice until you wait a long time, finish the simulation, and find some unreasonable result.

---

background-image: url(https://darkwebnews.com/wp-content/uploads/2017/03/3-main-os-300x244.png) 
background-size: 300px 
background-position: 95% 90%

# Run GNU MCSim in Windows

.font140[
*GNU MCSim* is a simulation package, written in C, which can run under different platforms (GNU/Linux, MacOS, and Windows).

However, the basic tools in the Windows system are not available to build and run GNU MCSim. It needs a bit more extra steps to install and execute it.

**Therefore...**
]

???

The GNU MCSim can run under different platforms, include Linux, Windows, and MacOS. This is one of the additional advantages of MCSim.

But it needs additional setting to run it under Windows because Windows system is a relatively different environment than MacOS and Linux.

So we need additional setting to finish the installation, such as install the compiler to compile the source code to the executable program.

---

# Run GNU MCSim in Windows

.font120[
- Prof. Weihsueh Chiu proposed a practical method using **minGW** to install it (<https://www.gnu.org/software/mcsim/mcsim_with_minGW.pdf>).

- Dr. Frederic Bois also provide an alternative method to compile and run GNU MCSim through Rtools. This concept called "MCSim under R".

- Dr. Nan-Hung Hsieh developed an installation function in R package **pksensi** (<https://cran.r-project.org/web/packages/pksensi/index.html>) to help users easily install GNU MCSim through this function across platforms.

Here, we proposed an additional idea to run GNU MCSim in **RStudio**, the integrated development environment (IDE) for R user. This project aims to help beginner write and run GNU MCSim's model code in RStudio IDE.
]

???

Since most of the people in toxicology filed mainly used and familiar with Windows system, therefore, Prof. Chiu proposed a practical solution to install MCSim in the minGW program.

The MinGW is a small Linux program that includes the compiler and command line interface so that the Windows user can execute the MCSim in this sandbox.

Dr. Frederic Bois proposed an alternative solution through install the C compiler from Rtools.

Based on this idea, I developed an installation function in R package pksensi to help user install MCSim through MCSim across the platform including Windows. And now, I want to extend this idea into RStudio IDE, because it's a powerful interface for R user. It can use to edit the model and simulation files in this interface as well.

---

background-image: url(https://i.ibb.co/S5YdcF7/download.png)
background-size: 650px
background-position: 50% 70%

# GNU MCSim under R

An open R project that aims to help beginner (especially Windows user) run GNU MCSim in **RStudio IDE**. All resources are stored in GitHub repo .font80[(https://github.com/nanhung/MCSim_under_R)].

???

The MCSim under R aims to help beginners especially Windows user to learn and run MCSim in the Windows system.

It just my side project. Also, I think RStudio is an excellent interface that is easy for people who has no programming experience to write and run their code. Currently, I still keep adding and improving the function of this project.

Hopefully, it will be easy for people to use MCSim in this way.

---

background-image: url(https://www.rstudio.com/wp-content/uploads/2018/10/RStudio-Logo-Flat.png)
background-size: 300px
background-position: 95% 95%

# RStudio

### Free and open-source integrated development environment

### Powerful and user friendly programming interface

### Designed to make it easy to write scripts

### Easy to view and interact with the objects

### R project with version control (e.g., git)

### Support cloud computing https://rstudio.cloud/

???

Some advantages about RStudio include it supports a lot of features in a user-friendly interface.

If you can not remember the R function name, it has the auto-completion function that can help you quickly write the script. You can also store and load MCSim output as an object and use this interface to check the basic information. It also has a plotting device to view your graphic.

It also supports version control and codebase organization in the form of projects. Also, it supports cloud computing, so you can also run MCSim in their cloud platform.

---

class:clear

background-image: url(https://i.ibb.co/tcBv3RF/RStudio-cloud.png)
background-size: contain

???

This is an example of RStudio cloud platform. You can run your R code in the console. It has the terminal to run the shell command if you are familiar with it.

It also has a sub window to let you edit your code. On the top right you can see what variable you have generated in the working environment.

You can also check the information by clicking the arrow button. Besides, you can see the functions that can be used to run MCSim or an additional application.

---

background-image: url(https://files.explosm.net/comics/comicsavegamenew.png)
background-size: 400px
background-position: 60% 70%

# Git

### - Manage your code (model, input, R script)

### - Transfer your file (through GitHub or GitLab)

### - Collaboration work

???

Git is a distributed version control system for tracking changes in the source code. The advantage of using it is it can help you track your model code, input code, and R script.

The reason to use Git is you might frequently modify your model or your input data. But if you make some mistake in your modification, this tools is the best way to help you track your revision.

The other advantage is it will be convenient for you to transfer your file from local computer to high-performance computer or other cloud platforms. Also, it is an effective way to collaborate on the development project.

---

# How to use GNU MCSim with R(Studio)?

---

# Overview

The *GNU MCSim* consists in two pieces, a **model generator** and a **simulation engine**:

<hr>

The model generator, **"mod"**

- Created to facilitate structural model definition and maintenance, while keeping execution time short. You can code your model using a simplified syntax and use mod to translate it to C (`model.c`).

The simulation engine, **"sim"**

- A set of routines which are linked to your model during compilation to produce executable program (`mcsim.model.exe`). After that, you can run simulations of your model under a variety of conditions, specify an associated statistical model, and perform simulations.

???

The GNU MCSim is constructed by two pieces, one is a model generator, and the other one is a simulation engine.

On the first step, the files in "mod" folder will create the MCSim program that can translate the simple model structure to C language. So the users don't need to learn C language to understand how to build the model. The syntax in MCSim is easier than C.

The second step is to use the files in the sim folder to compile the C model file to the executable program. After that, you can use your defined simulation files to make the different types of simulation as I mentioned in the previous slides. In addition, this program is portable so you can run it with input file in another PC or workstation.

---

# Workflow (GNU MCSim under R)

The source code of *GNU MCSim* are put into **"mod"** and **"sim"** folders. In addition, we need two types of files a **"model-file"** (model structure and default parameter values) and an **"input-file"** (run specific parameter values/distributions and/or observation data)

1. Making GNU MCSim program

Use the files in **"mod"** folder to

- build MCSim program named `mod.exe` (This only needs to be done once)

2. Build model program 
  
  Use the files in **"sim"** folder to

- build model program (&ast;.exe) with (1) `mod.exe` and (2) **"model-file"**

2. Run simulation 
  
  - Use model program and **"input-file"** to run simulation and generate result.

???

Generally, I separate the MCSim under R workflow to three part. The first part is to generate the MCSim program, which calls "mod.exe". This program is used to translate the model code that was written based on MCSim syntax and translate to C.

The first step only needs to done once unless the "mod.exe" file has been deleted by mistake.

The second step is to build the model program. This step needs the mod.exe file that was generated from the previous step. Also, we need a model-file that was created by the MCSim user. Then, we can use the source file in the sim folder to build the model program. Finally, the model program can be used to perform the different simulation based on the defined user input file.

---

background-image: url(https://i.ibb.co/bb9xS38/flowchart.png)
background-size: contain

# Overall Workflow

???

This an overall workflow to show each step from make a program to input and simulation. In this project, we can use R function to perform the simulation.

But this function can only work in R. If you need to run MCMC, I still recommend you to learn some command in Unix shell, because most of the high-performance computers are operated with Linux system. And it will be easy to use shell command in terminal.

In this workflow, you can modify all of the source code to run simulation if you want.

---

# Syntax of the model description file

```r
# Model description file (this is a comment)

States = { 
 <state variables for the model, such as quantity> 
}
Outputs = { 
 <output variables, such as concentration> 
}
Inputs = { 
 <input variables, such as exposure dose>
}
Initialize {
 <Equations for initializing or scaling model parameters>
}
Dynamics {
 <Equations for computing derivatives of the state variables>
}
CalcOutputs {
 <Equations for computing output variables>
}
End. # mandatory ending keyword
```
]

???

This is a general format of the model description file. The model description file is a text file that consists of several sections, including global declarations. It is used to define the default value of the input parameters.  
The state is used to define the variables of the model. The outputs are used to determine which output variable that you will estimate. For example, the state variable is the quantity of the chemical in blood or body tissues.  
The outputs section is used to define the estimated concentration. The input section is used to describe the exposure, so the user can use the defined input that can be based on the exposure route include inhalation, oral intake, and dermal contact. The dynamic section is used to specified the ordinary differential equation.   
The last one is the calculated output for computing derivatives of the state variables. If the user has additional output variable that will put the equation to state the output in this section.

---

# Example of model description file

States = {A_central, A_periph}
Inputs = {Dose}
Outputs = {C_central}

# Structural model parameters
k_12 = 1.02;
k_21 = 0.15;
k_10 = 0.18;
V_central = 58.2;

# Measurement error 
Ve_C_central = 1;

# Initalization
Initialize {
  A_central = Dose;
}

# Dynamics
Dynamics {
  # Central compartment quantity
  dt(A_central) = k_21 * A_periph - k_12 * A_central - k_10 * A_central;
  # Peripheral compartment quantity 
  dt(A_periph) = k_12 * A_central - k_21 * A_periph;
}

CalcOutputs { 
	C_central = A_central / V_central ; 
}

End.
```
]

???

It is an example of two-compartment model; it's a relatively simple example to understand how to write model code for PBPK modeling. In the section of the state, it has only two state variables, one is a central compartment, the other is the peripheral compartment. In the input is the given dose.   
The output section is the predicted concentration in centration compartment. The global variables in this model include 3 rate constants, one volume parameter for the central compartment.   
The last one is the measurement error, and this parameter is used to assume error distribution between data and model predictions. This error may include variability due to measurement error, intra-individual and intra-study heterogeneity, as well as model misspecification.  
In this model, the only initialization is setting the initial condition of the central compartment to the given dose. In the dynamic section, it was constructed by two ordinary differential equation. Then, the calculated output is used quantity in central compartment divided by the central volume to estimate the concentration.

---

# General syntax

Variable assignments

```r
<variable-name> = <constant-value-or-expression> ;
```

Colon conditional assignments

```r
<variable-name> = (<test> ? <value-if-true> : <value-if-false>);
```

For example

```r
Adjusted_param = (Input_var > 0.0 ? Param * 1.1 : Param);
```

.footnote[
Some other assignments can be found in  [GNU MCSim's user manual 5.3.1](https://www.gnu.org/software/mcsim/mcsim.html#Syntax-of-mod-files)
]

???

To assign the variable, the general method is used the equal sign to specify the variable with constant value or expression. It can also use the if-else statement to define the variable.

In this example, if the input variable greater than 0 the parameter value will be 1.1 times the parameter value. Otherwise, the parameter will be the given value in the estimation.

The best way to learn how to use this syntax is to read the example code in MCSim's example folder. There are a lot of example code that you can use them to do the test and run.

---

# Comments on style

> For your model file to be **readable** and **understandable**.

- All variable names begin with a capital letter followed by meaningful lower case subscripts.
- Where two subscripts are necessary, they can be separated by an underscore, such as in `PC_fat`.
- Where there is only one subscript an underscore can still be used to increase readability as in `Q_fat`.
- Where two words are used in combination to name one item, they can be separated visually by capitalizing each word, as in `BodyWt`.

.footnote[
Some other contents can be found in  [GNU MCSim's user manual 5.3.11](https://www.gnu.org/software/mcsim/mcsim.html#Syntax-of-mod-files)
]

???

The other thing I'd like to mention here is the style in the script file. It's crucial to make your file readable and understandable because you might publish this code on your paper in the future. It can help your colleague and people from other places easily use your code without any difficulty.

Generally, in PBPK model we can use A as quantity, Q as flow rate, V as volume, PC as partition coefficient and C as concentration.

It will be better to have a consistent notation that makes sense to you and other people. If you have to suspend work for a month or two and then come back to work on it, you have to add some comments on your file.

It can decrease the probability of making mistakes. If all of the equations are coded with a consistent, logical convention, you don't need to spend extra time to remember what you did. Also, use comments to annotate your code! make sure your comments are accurate and update them when you change your code.

---

background-image: url(https://irudnyts.github.io/images/posts/2019-01-14-r-coding-style-guide/assignment.jpg)
background-size: 350px
background-position: 95% 20%

# Comments on style (R)

```
# Good
x <- 5
# Bad
x = 5
```

**Without spacing**

```
# Good
average <- mean(feet / 12 + inches, na.rm = TRUE)

# Bad
average<-mean(feet/12+inches,na.rm=TRUE)
```

**Put more than one statement (command) per line**

```
# Good
x <- 1
x <- x + 1
 
# Bad 
x <- 1; x <- x + 1
```
]

.font80[
> “Good coding style is like using correct punctuation.   
> You can manage without it, but it sure makes things easier to read.”  
> — Hadley Wickham, Chief Scientist @RStudio
]

.right[
.font60[
[source 1](http://adv-r.had.co.nz/Style.html) | [source 2](https://irudnyts.github.io/r-coding-style-guide/)
]
]

???

It is the same recommendation for R coding style. There are some example style guilds. If you can follow these guides, it will be easy for you and other people to use or reproduce the result from your script file. Because computer language is also a tool that allows human beings to interact and communicate with each other.

It's not easy to learn and apply all of this knowledge. But You will have the accomplishment if you can master it. And there is a lot of fun in programming and modeling.

---

# Syntax of (simulation) input-file

## For the basic simulation

```r
# Input-file (text after # are comments)
<Global assignments and specifications>
Simulation {
 <Specifications for first simulation>
}
Simulation {
 <Specifications for second simulation>
}
# Unlimited number of simulation specifications
End. # Mandatory End keyword. Everything after this line is ignored
```

???

Moving back to the MCSim syntax, this is an example of basic simulation. The only thing you need to do is provide the given condition in your simulation, which is the output time points and the output variables.

You can also use multiple sections to define your simulation. For example, the simulation one can be used to specify the low dose exposure scenario and the second section can be used to specified the high dose exposure scenario.

---

# Syntax of (simulation) input-file

## For MCMC simulation

```r
# Input-file
<Global assignments and specifications>
Level {
 # Up to 10 levels of hierarchy
 Simulation {
 <Specifications and data for first simulation>
 }
 Simulation {
 <Specifications and data for second simulation>
 }
 # Unlimited number of simulation specifications
} # end Level
End. # Mandatory keyword.
```

[`MCMC()` specification](https://www.gnu.org/software/mcsim/mcsim.html#MCMC_0028_0029-specification)

???

For the Markov chain Monte Carlo simulation, instead of the basic simulation. We need to define the Level sections and Data specifications.

In the <Global assignments and specifications>, we need to assign priors and likelihoods through the Distrib() statement.

In the level section, we can define the population level, group level, and individual level to define the inter-individual or intra-individual.

In each section, we can further define the population parameter or local parameter in parameter sampling.

---

# Example of (simulation) input-file

Simulation {
  Dose = 509;
  Print (C_central, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 23);
}

End. 
```
]

```r
mcsim(model = "digoxin.model.R", input = "digoxin.in.R", dir = "modeling/digoxin")
```

```
## Execute: ./mcsim.digoxin.model.R.exe modeling/digoxin/digoxin.in.R
```

```
##    Time C_central
## 1   0.5  4.910300
## 2   1.0  2.933400
## 3   2.0  1.383300
## 4   3.0  0.960978
## 5   4.0  0.837285
## 6   5.0  0.792841
## 7   6.0  0.769599
## 8   7.0  0.752196
## 9   8.0  0.736565
## 10 23.0  0.543027
```
]

???

For the digoxin case, we use 2 compartment model that I mentioned in the previous slide to perform the simulation. Here we give two statements, the first one is the given dose. This is the initial condition of the central compartment.

The print statement is used to set the output variable, time points. In this simulation, we focus on the concentration in the central compartment in the 24-hour after drug intake. Our result shows that in the first half hour the predicted concentration is 4.9 mg/L. Then, the concentration decreasing to 0.5 in the 23-hour.

In addition, you can see I put some comment on the top, the first line is to specify the file name. The second line is used to illustrate how to run the model, which model code we need to use. Use this comment can help you memorize which model file that you need to used to run this input file.

---

# Example of (simulation) input-file

MCMC ("MCMC_default.out","", # name of output and restart file
      "",                    # name of data file
      2000,0,                # iterations, simTypeFlag,
      10,2000,               # printing frequency, iters to print
      10101010);             # random seed (default)

Level { # top level
  Distrib(k_12, LogUniform, 0.01, 10);
  Distrib(k_21, LogUniform, 0.01, 10);
  Distrib(k_10, LogUniform, 0.01, 10);
  Distrib(V_central, TruncNormal, 50, 5, 40, 60);
  Distrib(Ve_C_central, LogUniform, 0.01, 0.5); # 10% to 70% residual error
  
  Likelihood(C_central , Normal, Prediction(C_central) , Ve_C_central);
  
  Simulation {
  Dose = 509;
  Print (C_central, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 23);
  Data (C_central, 4.6244, 2.7654, 1.3224, 0.9563, 0.8843, 0.8648, 0.8363, 0.7478, 0.7232, 0.5655);
  }
} 
End. 
```
]

???

This is the example of input file for MCMC simulation. There is an output file named "sim.out", the second assignment is used to put the restart file to the basic checking of the simulation result of continuous run the MCMC simulation if the previous simulation was accidentally terminate. 
The data file assignment is used to set the input data. But according to MCSim manual, it recommends user use Data() specifications in input-file rather that the data file, which is much more error-prone. Then we need to give the number of iterations.

The next one is the flag that is used to select the simulation types. This flag can be defined from 0 to 4. The detail will provide in the following class. The printing frequency is setting to 10 in the current input-file, this setting is usually used to prevent the large output file size in the long iterations with large experiment data.   
The next assignment is iterations to print is the number of final iterations for which output is required. In this case, if I used 1000 in this assignment. The printing of output will start from 1000 instead of initial iterations.   
The last assignment is the random seed. The MCMC is used pseudo-random number generator, so you need to modify this number to create the different MCMC chains and simulation result. Also, this value is used to make sure each result can be reproduced whenever you run the simulation.

The next section is level, In this case, we only have one level to estimate the parameter posterior. And we used TruncNormal to assigned the distribution volume, because we have the basic knowledge about the possible range, but for the rate constant, I have no idea about this parameter. So I used LogUniform distribution and set a wider range.  
 For the measurement error, we assumed we the error are ranged from 10% to 70% among data and prediction. Then, in the simulation section, I put the experiment data include measurement time and concentration.

---

class:clear

```r
out <- mcsim(model = "digoxin.model.R", input = "digoxin_mcmc.in.R", dir = "modeling/digoxin")
```

```
## * Create 'MCMC.check.out' from the last iteration.
```

```r
head(out)
```

```
##   iter   k_12.1.  k_21.1. k_10.1. V_central.1. Ve_C_central.1.   LnPrior
## 1    0 0.0578463 0.367589 1.10359      49.0648        0.180277 -3.225252
## 2    1 0.0578463 0.367589 1.10359      49.0648        0.180277 -3.225252
## 3    2 0.0578463 0.367589 1.10359      51.8269        0.180277 -3.274512
## 4    3 0.0578463 0.367589 1.10359      53.1764        0.232568 -3.664244
## 5    4 0.0578463 0.367589 1.10359      53.3446        0.232568 -3.686171
## 6    5 0.0578463 0.367589 1.10359      53.3446        0.232568 -3.686171
##      LnData LnPosterior
## 1 -71.15186   -74.37711
## 2 -71.15186   -74.37711
## 3 -60.08674   -63.36125
## 4 -33.27581   -36.94005
## 5 -33.04232   -36.72850
## 6 -33.04232   -36.72850
```

```r
tail(out)
```

```
##      iter k_12.1.  k_21.1.  k_10.1. V_central.1. Ve_C_central.1.   LnPrior
## 1996 1995 1.10086 0.173742 0.176099      59.6520        0.060332 -4.337722
## 1997 1996 1.10086 0.177757 0.176099      59.3366        0.030046 -3.543681
## 1998 1997 1.11723 0.177757 0.176099      59.5178        0.030046 -3.626767
## 1999 1998 1.11723 0.177757 0.176099      59.3709        0.030046 -3.571257
## 2000 1999 1.11469 0.179285 0.176099      59.6882        0.030046 -3.698514
## 2001 2000 1.09671 0.179163 0.176099      59.6882        0.030046 -3.681576
##        LnData LnPosterior
## 1996 17.69351    13.35578
## 1997 18.41824    14.87456
## 1998 19.04836    15.42160
## 1999 19.30200    15.73074
## 2000 18.50762    14.80911
## 2001 18.46795    14.78638
```

]

???

Here shows the output result, as you can see, there are 2000 iterations in this simulation. In each simulation, it will estimate the posterior parameter value. According to the result from the last five iterations, you can find that the parameters value are relatively stable than the beginning. Such as ...

The likelihood are greater than beginning as well. But this is just the example we will explain more detail in the following tutorial.

---

# Distribution functions

.font80[
- **InvGamma** (inverse gamma distribution), needs two strictly positive real parameters: the shape and the scale.
- **LogNormal**, takes two reals numbers as parameters: the geometric mean (exponential of the mean in log-space) and the geometric standard deviation (exponential, strictly superior to 1, of the standard deviation in log-space).
- **LogUniform** with two shape parameters: the minimum and the maximum of the sampling range (real numbers) in natural space.
- **Normal** takes two reals numbers as parameters: the mean and the standard deviation, the latter being strictly positive.
- **Normal_v** is also the normal distribution with the variance instead of the standard deviation as second parameter. 
- **TruncNormal** (truncated normal distribution), takes four real parameters: the mean, the standard deviation (strictly positive), the minimum and the maximum.
- **StudentT**, requires three parameters: its number of degrees of freedom (an integer), its mean, and its standard deviation.
- **TruncLogNormal** (truncated lognormal distribution), uses four real numbers: the geometric mean and geometric standard deviation (strictly superior to 1)
- **LogNormal_v**, is the lognormal distribution with the variance (in log space!) instead of the standard deviation as second parameter. 
]

.footnote[
More functions in [GNU MCSim User’s Manual](https://www.gnu.org/software/mcsim/mcsim.html#Distrib_0028_0029-specification)
]

???

GNU MCSim also includes more than 20 distribution functions that can be used to define the parameter settings. Here are some common distributions that might frequently use in the simulation.

For example, the log uniform and student T can be used to define the measurement error and the detection limit. Usually, we used inverse Gamma to describe the population variance. Also, the normal, lognormal, and uniform are the most common distributions to describe the parameter prior and posterior.

---

# Input functions

These functions can use to different exposure types

PerDose(<magnitude>, <period>, <initial-time>, <exposure-time>);

- PerExp(): # specifies a periodic exponential input.

PerExp(<magnitude>, <period>, <initial-time>, <decay-constant>);

- PerTransit(): models a delayed input mechanism

PerTransit(<magnitude>, <period>, <initial-time-in-period>, 
 <decay-constant>, <number-of-input-compartments>); 
 
 
- NDoses(): specifies a number of stepwise inputs of variable magnitude and their starting times
 
 NDoses(<n>, <list-of-magnitudes>, <list-of-initial-times>);

- Spikes(): specifies a number of instantaneous inputs of variable magnitude and their exact times of occurrence.
 
 Spikes(<n>, <list-of-magnitudes>, <list-of-times>);

```
]

???

Here is the list of supported input function in MCSim that can be used to describe the different exposure type. For example, the first one PerDose can be used to describe the periodic intake of the specific compound, so we can use this method to predict the steady state under the particular exposure scenario.

Besides, the NDoses function can let you used the different level of exposure and the starting time points based on the exposure scenario. Also, in pharmacology research, the spikes function can be used to describe the intravenous PK data.

---

# Main functions

Here are the R functions that can help you run GNU MCSim more easily. All R functions are defined in `function.R` in MCSim folder.

```r
makemcsim(model, dir = "modeling", deSolve = F)
```

- Preprocessing and compiling the model-file to the executable file as `makemcsim` in GNU MCSim. The `model` assignment is a string giving the name of the model-file (e.g., `"pbpk.model.R"`). The `deSolve` assignment is a logical factor to use **deSolve** package as an ODE solver.

- The default location of modeling files are setting at `modeling` folder. The loaction can change by re-assign `dir`.

---

# Main functions

```r
mcsim(model, input, dir = "modeling", parallel = F)
```

- Using the compiled program with the input-file to run the simulation. The `input` assignment is a string giving the name of the input-file (e.g., `"pbpk.in.R"`)

- This function can also automatically compile the model, if you forgot to use `makemcsim()` to create model program.

- Can use `parallel = T` if using parallel computing in MCMC model calibration.

???

In this MCSim under R project, I add some functions that can be used to make the model program and run MCSim through R function instead of the  shell command.

The first function is used to create a model program. The model program is the portable file so you can move and execute it in other directories.

There is an assignment to specified the name of the model file.  Also, the mcsim() function is used to run the simulation. Therefore, in addition to the model file, we need to assign the input-file to run the simulation.

Basically, the model and input files are put in the modeling folder. But when you create and save your model code, they will be saved under the MCSim_under_R folder as default. This two function can automatically move these file to the modeling folder. So you don't need to worry about this issue. The other feature of MCSim is it can generate the C language that can be executed through R deSolve package.

---

# Example of using **deSolve**

```r
library(deSolve)
model <- "digoxin.model.R"
makemcsim(model = model, deSolve = T, dir = "modeling/digoxin")
parms <- initParms() # Define parameter value 
newParms <- c(parms, Dose = 509) # Define input
Y <- initStates(parms = newParms) # Initial conditions
times <- c(0, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 23)
out <- ode(Y, times, func = "derivs", parms = parms, 
 dllname = model, 
 initfunc = "initmod", nout = 1, 
 outnames = "C_central")
out
```

```
##    time A_central A_periph C_central
## 1   0.0 509.00000   0.0000 8.7457045
## 2   0.5 285.78053 188.5568 4.9103185
## 3   1.0 170.72485 283.6368 2.9334166
## 4   2.0  80.50653 352.9739 1.3832736
## 5   3.0  55.92820 365.7309 0.9609657
## 6   4.0  48.72975 363.6315 0.8372809
## 7   5.0  46.14326 357.7117 0.7928394
## 8   6.0  44.79060 350.8890 0.7695980
## 9   7.0  43.77781 343.9332 0.7521961
## 10  8.0  42.86809 337.0456 0.7365651
## 11 23.0  31.60418 248.5552 0.5430271
```
]

```r
mcsim(model = "digoxin.model.R", 
      input = "digoxin.in.R", 
      dir = "modeling/digoxin")
```

]
???

This is an example of using deSolve package to make a straight simulation. In this approach, you don't need to create the input file, you can use the ode function from the deSolve package. The input information can be set through the R function. So you can view your setting condition through R function or RStudio. It's more convenient than the original method.

But if you want to do Monte Carlo simulation or global sensitivity analysis. I'll recommend to use the model program to have faster speed than the deSolve solver.

---

# Other functions

```r
set_PATH(PATH)
```
- Detecting, checking, and setting the C compiler in your computer. This process will automatically execute. The default PATH setting is `"c:/Rtools/mingw_32/bin"`.

```r
makemod()
```
- Creating MCSim program `mod.exe`.

```r
clear()
```
- Removing all executable and output files with extension `.exe`, `.out`, and `.perks` in the working directory. This function is used to ensure that all simulation process can be reproduced without misusing the old version of the file with the same file name. This function will not remove `mod.exe`.

```r
report()
```
- Reporting the system setting. 
]

???

These functions are not the main functions. They are used to conduct the basic setting, for instance, create the 'mod.exe' file or setting the Rtools path to use C compiler.

In addition, the clear() function is used to clean the file with .exe, .out and .perks. The reason to use this function is it will be better to re-run the full process to generate the result instead of using the old version.

Sometimes, you might forget that you have revised the model structure. It's the safe way to make quality assurance of your model output.

---

# Example: linear modeling

model-file

Outputs = {y}

# Model Parameters
A = 0; # Default value of intercept
B = 1; # Default value of slope

# Statistical parameter
SD_true = 0;

CalcOutputs { 
  y = A + B * t + NormalRandom(0,SD_true); 
}

End. 
```
]]

input-file

Simulation { # 1 simple simulation
  
  A  = 1; # given value of intercept 
  B  = 2; # given value of slope 
  SD_true = 2; # given SD of noise 
  
  PrintStep (y, 0, 10, 1); 
}

END.
```
]]

???

This is an additional example. We use linear model as an example, the model and input files are included in the modeling folder.  
Basically, it includes some elements that I mentioned in the previous instruction. You will be able to understand and revise this structure if you want.  
Unlike the typical linear modeling, this case adds the random noise form statistical parameter SD_true in this simulation.

---

# Example: linear modeling

A simple way to store the results in the output variable and check it,

```r
out <- mcsim(model = "linear.model.R", input = "linear.in.R")
```

```
## * Created executable program 'mcsim.linear.model.R.exe'.
```

```
## Execute: ./mcsim.linear.model.R.exe modeling/linear.in.R
```

```r
out
```

```
##    Time         y
## 1     0 -0.415609
## 2     1 -1.430340
## 3     2  4.144040
## 4     3  7.535080
## 5     4  9.517630
## 6     5 10.871900
## 7     6 13.735700
## 8     7 13.075000
## 9     8 16.095100
## 10    9 16.816300
## 11   10 21.300200
```

???

Same as the digoxin case, the output can store as an object. It's an easy way to check the output result.   
And if you use RStudio, you can interact your output result by clicking the output object.

---

# Example: linear modeling

If you forgot to assign a variable to store your output, you can use `read.delim()` to read the output file as,

```r
out <- read.delim(file = "sim.out", skip = 1)
out
```

**Question: why `skip = 1`?**

???

If you forgot to assign the object to store the simulation output, you can use the R base function to read the output file.

Based on the default setting, the output data will be stored under the text format. So you can open this text file to check the result or use R to read it and do additional analysis or visualization.

---

# Example: linear modeling

Visualization the simulation result by R base plot and ggplot

```r
plot(x=out$Time, y=out$y)
abline(a=1, b=2)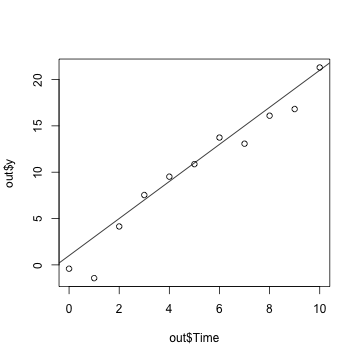
```

![](190418_tutorial_files/figure-html/unnamed-chunk-13-1.png)

]]

```r
library(ggplot2)
ggplot(out, aes(x=Time, y=y)) + 
  geom_point() +
  geom_abline(intercept = 1, slope = 2)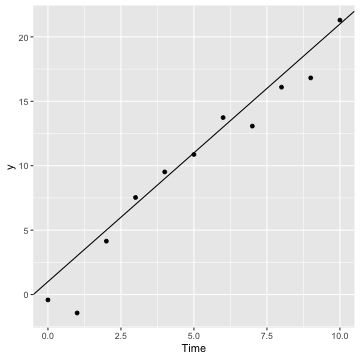
```

![](190418_tutorial_files/figure-html/unnamed-chunk-14-1.png)

]]

???

To visualize or plot your result, the simple way is to use the base R plot, just like the R script from the left-hand side, but if you want to make a pretty plot, you can use ggplot to generate the figure just like the ggplot on the right-hand side.

From this result, we can find the simulated data have a linear relationship with the given slope and intercept. Since it considers the random noise, the simulated data is not the perfect linear curve.

---

# Additional R packages for analysis

[data.table](https://cran.r-project.org/web/packages/data.table/index.html) - Fast reading of large output file, especially from MCMC with long iterations and high dimensional parameter space.

[tidyverse](https://cran.r-project.org/web/packages/tidyverse/index.html) - Powerful data science toolbox that can use to manipulate (`dplyr`) and plot (`ggplot`) the simulation result.

[sensitivity](https://cran.r-project.org/web/packages/sensitivity/index.html) - A collection of functions for factor screening, global sensitivity analysis and reliability sensitivity analysis.

[pksensi](https://cran.r-project.org/web/packages/pksensi/index.html) - Applying the global sensitivity analysis (eFAST) workflow to investigate the parameter uncertainty and sensitivity in pharmacokinetic (PK) models.

[bayesplot](https://cran.r-project.org/web/packages/bayesplot/index.html) - Plotting functions for posterior analysis.

[rstan](https://cran.r-project.org/web/packages/rstan/index.html) - Diagnose the simulation result from MCMC.

```r
# Quick installation
pkgs <- c("bayesplot", "data.table", "pksensi", "rstan", "sensitivity", "tidyverse")
install.packages(pkgs)
```

???

Here I want to provide the information about some useful package that you might need to analyze the result from MCSim.

The data.table and tidyverse are the useful data science tool to read and manipulate the output result from MCSim. The ggplot provided the more elegant function to visualize the data and predicted results.

The sensitivity package and pksensi are the packages that can be used to perform sensitivity analysis.

The bayesplot and rstan can be used to diagnose and visualize the result from MCMC simulation to perform posterior analysis.

---

background-image: url(https://i.ibb.co/ZLRrNJy/syntaxhighlight.png)
background-size: 620px
background-position: 50% 90%

# Tips of MCSim under R(Studio)

### Code edit
Generally, the GNU MCSim used `.model` and `.in` as the extension to name the model- and input-file. However, RStudio doesn't support the syntax highlight for these extensions. You can add `.R` as the extension for these files to help you edit your model or input in RStudio with syntax highlighting. Also, it can help you format your code in the code bracket.

???

In this MCSim under R project, I use .R as extenstion instead of the typical .model and .in to give the model and in put file name ...

---

# Tips for MCSim under R(Studio)

### Example & input
Some example R scripts will put into the `example` folder. To run *GNU MCSim* in model simulation, we need to have two types of file (1) **model** and (2) **input** files. The syntax of the model description file can find in [*GNU MCSim* User's Manual](https://www.gnu.org/software/mcsim/mcsim.html). All example `model` and `input` files are located in the `modeling` folder.

.font80[
[&ast;] You don't need to move your model- or input-file to *modeling* folder, manually.   
Just run `mcsim(model-file, input-file)` after you finish your code, then they will be moved to **modeling** folder.
]

???

In addition, I put some example model and input file in the modeling folder that can be used to run and learn the basic simulation.

The running r scripts are put in the example folder. But currently, I only have two example files. But I will continuously add more example in this folder.

---

# Following courses

- Tutorial 2: **MC simulation and sensitivity analysis** (5/16)

- Tutorial 3: **Bayesian MCMC calibration** (5/23)
]

<center>
.font160[
It's your turn to **run** it!
]

![](https://slides.yihui.name/gif/pass-chase.gif)

???

We have other courses that will be on April 25th ...

---

background-image: url(https://www.cantechletter.com/wp-content/uploads/2013/11/nate-silver-the-signal-and-the-noise.jpg)
background-size: 320px
background-position: 99% 95%

# Take away

- *GNU MCSim* & *R* are powerful tool in statistical computing and modeling

- We provide an alternative way to run *GNU MCSim* in **RStudio** that aim to help user learn and familiar with *GNU MCSim* workflow
]

<hr>

Meet problem? Please submit it to

- MCSim under R GitHub issues https://github.com/nanhung/MCSim_under_R/issues
- My email: nhsieh@cvm.tamu.edu